A sample-based phase algorithm for quantum computers
Abstract¶
In this work, we propose a quantum algorithm that applies arbitrary phase profiles to a quantum register meaning that it transforms the state of the register to . The important property of the algorithm is that instead of using a unitary operator that applies the phase directly to the initial state, it uses a secondary register initialized as to apply the phase. This algorithm uses copies of this secondary state to apply a phase profile to that is a function of the secondary state as where α is an arbitrary coefficient. Therefore, this algorithm allows us to apply different phases to a quantum register using different input states as the secondary register. It is also important to note that the algorithm derived in this work is agnostic about the input states and , therefore, the implementation of the algorithm itself does not change for applying different phase profiles and we only need to change the input state to apply the corresponding phases.
2Introduction¶
Quantum computers can be used to store and process information. For particular problems such as prime number factorization Shor (1997), search and optimization Grover (1996), specific quantum algorithms have been discovered that can solve the problems with lower computational complexity compared to the best-known counterpart classical solutions Montanaro (2016). Such quantum algorithms leverage the properties of quantum systems such as superposition and entanglement that enable them to achieve performance boost and memory efficiency Nielsen & Chuang (2010).
In this work, our goal is to find an efficient quantum algorithm for applying arbitrary phase profiles to quantum registers. This problem translates to transforming the initial state of a quantum register as
to
for any real-valued function .
Phase profiles are particularly important for simulating physical systems. The time evolution of many systems can be modeled using the change of phases of the initial state. In the following, we will discuss a quantum and a classical case where the time evolution is described via changes in the phases of the initial state.
We start by discussing the unitary evolution in quantum mechanics as an example. Let us assume we have a quantum mechanical system described using the state and the Hamiltonian of the system is , where the Hamiltonian is a function of the momentum operator as
This assumption means that the Hamiltonian commutes with the momentum operator
thus we can find a set of common basis states for them, and the Hamiltonian can be diagonalized as
where are the momentum basis states.
The initial state can also be described in the momentum basis as
where are the probability amplitudes of the state being in the momentum basis state.
The evolution of the system for time can be modeled using the unitary operator
This means we can simulate the time evolution of the initial system by applying a phase profile to the initial probability amplitudes as
where the phase profile in this case is
Phases also play an important role in the evolution of classical systems. One example in the field of optics is the propagation of a light beam in the Fresnel approximation Saleh & Teich (1991).
Let us assume a field to be the initial field distribution of an electromagnetic wave in the transverse plane where the direction of the motion of the beam is the axis.
The propagation of the light beam after the distance in the Fresnel approximation can be simulated via the following steps:
Applying Fourier transformation to
Multiplying the calculated Fourier spectrum by the Fresnel transfer function . The Fresnel transfer function consists of phase terms
where is the wave number of the field and λ is the wavelength.
Applying this transfer function to the spectrum, we will have
Finally, the propagated field at the distance is calculated via an inverse Fourier transformation
In this example, the simulation was modeled using the combination of Fourier transformations and applying a phase profile corresponding to the function
These were two examples to show the importance of the phase problem for the simulation of the evolution of physical systems over time. Therefore, a generic algorithm that can apply an arbitrary phase profile to signals stored in the memory of a computer can simulate various physical systems.
As we will see in this thesis, applying arbitrary phases in quantum computers is not as straightforward as in classical computers. The central reason for this difficulty is rooted in the way information is stored in quantum memories. We will discuss the details of the problem in the following sections.
2.1The outline of the thesis¶
In writing this thesis, we assume the reader possesses the standard knowledge of quantum mechanics and a basic knowledge of quantum computers. However, we will review the important basic concepts of quantum computers before moving on to solving the problem in order to make a solid ground for the upcoming derivations.
This thesis report is structured as follows. In Section 3, we review the basics of quantum computers and describe how we generally model problems and store the information in quantum memories. In Section 4, we introduce the phase problem using the modeling language we established in the previous section. In this section, we will also discuss the considerations we need to pay attention to in the modeling of the problem which will allow us to generalize the problem in several iterations.
Next in Section 5, we will start solving the problem defined in the previous section. As we will see, we will derive the complete solution in two major steps. In the first step, we will find a quantum phase operator that works in certain approximated conditions. We call this operator the partial phase operator. Next, we will use this operator in a larger algorithm which enables us to overcome the limitations of the previous approximations. This algorithm will be able to apply arbitrary phase profiles and we call it the sample-based phase algorithm. This section also includes the analysis of the error and the accuracy of the algorithm as well as an actual implementation of the algorithm using the standard circuit model of quantum computers.
After deriving the algorithm, we will choose a specific problem to simulate using the algorithm and characterize the errors in that case in Section 6. This will allow us to demonstrate and verify the derivations of the previous section.
3Theory¶
The goal of this section is to introduce quantum computers and to provide the necessary mathematical framework for the derivations that come in the next sections. We start by discussing concepts such as qubits and quantum memories and introduce the approach we use to encode signals and fields in the memory of a quantum computer.
3.1Quantum memories¶
Quantum memories are one of the cores of quantum computers; they play the role of storing the values of our initial parameters of a problem. A quantum computer processes that information to calculate the solution to the problem. The information processing in quantum computers is done via unitary operations acting on the memory. To use quantum computers to solve a problem, we have to find a way to store the initial parameters in the quantum memory and find a sequence of unitary operations that can calculate the solution of the problem using that initial values.
In order to understand this process, we need to study the main properties of quantum memories and qubits. The model of quantum computers we introduce here will allow us to continue with the derivation of the phase algorithm in the upcoming sections. We start by introducing the units of a quantum memory which is a qubit.
Qubits¶
The units of quantum memories are qubits. A qubit is defined as a 2-dimensional quantum system. This means it is modeled as a vector living in a two-dimensional Hilbert space. We know from linear algebra that a two-dimensional Hilbert space is spanned via two orthogonal basis states; we name one of the basis states and the other one .
And because any linear superposition of the basis states is a valid state for the qubit, in general, a qubit can be described as the following sum of the basis states
where and are two complex probability amplitudes of the qubit being in the corresponding basis state and .
When studying quantum algorithms, we usually do not assume any physical system that is used for the realization of the qubit and define them in the abstract way as we have done here. This enables us to study quantum algorithms agnostic of the physical implementation of the quantum computer. Therefore, algorithms should in principle work on any realization of quantum computers that can provide such qubits. However, one can think of many physical systems such as the spin of an electron or the polarization of a photon to be described as a two-dimensional quantum system as we defined for the qubit.
We note that the normalization principle of quantum states forces the equation . Also, the choice of the global phase is arbitrary because phases does not change the features of a quantum state. Hence, we have to consider reducing two real-value degrees of freedom from the two complex numbers . However, we will see in the next section that when we put qubit units together to form a quantum memory, this consideration will quickly become negligible as the degrees of freedom of the compound memory will increase exponentially with the number of qubits; therefore, decreasing a constant two real numbers from the overall degrees of freedom can be neglected.
Compound memories¶
Similar to classical computers where a large memory is made of units (bits), we can put several qubits, as units of memory in a quantum computer, together to form a compound memory. We use the terms register or memory to describe a system consisting of several units of memory.
Let us assume we have a quantum register consisting of qubits. We name these qubits , , , . We know from quantum mechanics that a compound system is described using a Hilbert space which is the tensor product of the spaces of the individual sub-systems. This means that if we put these qubits together, the basis states of the compound memory will be
where each can be either 0 or 1. Note that we can count the number of these basis states which is . Furthermore, the state of the register can be in a superposition of all these basis states
where is the probability amplitude of the register being in the corresponding compound basis state. We can see that in this case, the state of the system is described using complex numbers and in general, the qubits can be in an entangled state.
Similar to the note we mentioned when introducing qubits, we should also decrease two real-valued (equivalent to one complex-valued) degrees of freedom of describing the state of the register because of the normalization principle and the global phase. This means that the number of complex parameters needed to describe a quantum register consisting of qubits is
As we can see, the consideration coming from normalization and the global phase can be neglected in various cases because of the exponential relation .
The basis index and binary encoding¶
Now that we have our compound memory, we can choose a binary encoding to map each basis state
to a unique index
We can choose between different encodings based on the nature and the requirements of the problem.
If we only work with positive indices, we can choose unsigned encoding as
which results in the range of for possible values of γ.
Whereas in order to have both negative and positive indices, we can use two’s-complement encoding as
In this case, γ can represent any integer in the range of .
After we choose a binary encoding for the basis state indices, we can reinterpret (17) as
where the summation on γ is over all possible values corresponding to the chosen encoding. For example in the case of two’s-complement encoding, it translates to
In any case, there are probability amplitudes that describe the quantum register.
Sampling and storing a signal in quantum registers¶
Now that we have chosen a binary encoding for the basis states, the next step is to store a signal in the quantum register.
Let us assume we have sampled a signal at discrete points using the uniform sampling method; it means that we have chosen a fixed sampling period and extracted the function values at points .
Any choice of normalized complex numbers corresponds to a valid state for the quantum register in (23). This means that we can store sample points of a normalized complex signal by initializing the quantum register in a state with probability amplitudes as
This initialization allows us to store numbers in an -qubit quantum register. Compared to classical registers, we have achieved exponential efficiency in memory usage; because in classical registers, the number of degrees of freedom of the memory grows linearly with the number of the units (bits). Whereas in quantum registers, this growth is exponential with the number of units (qubits) as described in the previous sections.
The initialization problem¶
In the previous section, we mentioned that we can store complex numbers in an -qubit quantum register by initializing the register in a state corresponding to our desired signal.
We have to mention that the task of initialization is not trivial for all desired signals Schuld & Petruccione (2021). By definition, quantum computers are able to initialize a register in a non-entangled reset state such as
where all qubits start in the state.
The initialization problem deals with generating any desired state as described in (25) starting from the trivial reset state in (26). It is not straightforward how to initialize the register in any arbitrary state. We need to derive specific initializers for our input states or use the existing initializers from the literature. For example, we can name the Kitaev-Webb algorithm for initializing a Gaussian state Kitaev & Webb (2009).
The goal of this work is not to deal with the initialization problem; therefore, we generally assume the existence of an initializer for our desired initial input signals.
4Introducing the Problem¶
After discussing the preliminary theory, we are ready to state the problem and derive the solution in the following sections.
As briefly mentioned in the introduction, our goal is to apply arbitrary phase profiles to signals stored in a quantum computer.
Let us assume we have a quantum register with qubits initialized in an arbitrary state
where is the number of basis states of the memory and are the computational basis states. We might often leave out the upper and lower summation bounds to indicate the sum over all possible values as
We would like to be able to apply an arbitrary (real-valued) phase profile to this register, meaning to transform the state to
such that
One general approach to do that is to derive an operator for each phase profile that applies the desired transformation on the state as
Previously, we showed how this transformation can be done for the special case of polynomial phase profiles where for arbitrary α and values using polynomial phase operators Davani (2023)Cholsuk et al. (2023)Davani (2023). More specifically, we derived operators that apply the following transformation on the register
We call polynomial phase operators because they apply a phase to the wavefunction of the quantum register which is polynomial with respect to the basis index γ as .
We also note that the operator can be implemented using number of gates Davani (2023).
While polynomial phase profiles are very useful in many applications such as simulating Fresnel-approximated beam propagation (as discussed in the referenced work Cholsuk et al. (2023)Davani (2023)), there are many applications where we would like to apply arbitrary phase profiles and not just polynomial phases.
In principle, arbitrary phase profiles can be applied using the polynomial phase operators by Taylor-expanding at an arbitrary point and working with an approximated Taylor expansion. The Taylor expansion can be written as
If we keep the terms up to the -th order. We will end up with
which is a summation that includes polynomial terms where .
This means that the phase can be applied by combining operators and the total computational complexity will be .
We can see that for phase profiles where a low-order Taylor approximation is not accurate, we have to lower the approximation error by increasing . This is not ideal because for very large we the computational complexity increases as
This means that applying arbitrary phase profiles using this method is not efficient in practice.
The solution we propose in this work for applying arbitrary phase profiles is based on a different approach. We will discuss the approach in the following.
4.1The proposed solution¶
Instead of deriving an operator for each phase profile , we introduce a secondary register and propose an algorithm that uses the state encoded in the secondary register to apply arbitrary phase profiles to a primary register. This approach is inspired by the work of Lloyd et al. Lloyd et al. (2014) and the further investigation of that work by Kimmel et al. Kimmel et al. (2017) on the topic of sample-based Hamiltonian simulation.
Assuming we have a primary -qubit quantum register (we call it the register ) initialized in an arbitrary state as
and a secondary register (we call it the register ) with the same number of qubits as
What we propose is a quantum operator that acts on both registers together and applies a phase to the primary register (with a defined error) based on the secondary register as
We will discuss the exact formulation of the algorithm and the derivations in the following sections.
If we compare this to the approach discussed in (31), we realize that this algorithm corresponds to applying a phase profile equal to
This gives us the freedom of applying arbitrary phase profiles to the state as long as we can initialize the secondary register to a state corresponding to the probability amplitudes .
We must take several steps to derive the complete algorithm. First, we will find an operator that performs the transformation in (38) but with the assumption that α is small. To distinguish this case from the general case, we use a different letter Δ for the phase coefficient as . We define the smallness assumption such that therefore the square and higher powers of Δ are negligible in our derivations. Thus, the operator we derive in this case will apply the phase profile
to our primary register for small Δ.
We call this operator the partial phase operator. It uses one copy of the secondary state to perform the transformation.
Next, we use the partial phase operator iteratively using multiple copies of the state and apply the phase steps consecutively to the primary memory times to apply an overall phase of
This enables us to overcome the limitation of the assumption and to apply arbitrary phases as
where .
We call the final iterative algorithm the sample-based phase algorithm because it uses the samples of the encoded phase profile in a quantum register to apply arbitrary phases to a primary register.
We furthermore analyze the error introduced by this iterative approach and derive a relation for the required number of iterations based on the parameters of the problem such as α.
Now that we have introduced the main idea of this work, we progress to modeling the problem mathematically in the next section.
4.2Preliminary mathematical modeling¶
In this section, we start modeling the problem and discussing the preliminary points we must consider to do so. After the discussion, we restate the problem in its most generalized form and use this generalized form for our derivations in Section 5.
As discussed in the previous section, we assume that we have a primary register that we want to apply a phase to using the phase profile stored in a secondary register .
At first, we realize that this means we should search for an operator that acts on both registers together to be able to transform the primary register based on the state of the secondary register. In the ideal case, we can search for an operator that applies the following operation
where is the desired final state given as
and is the final state of the secondary register. We do not expect any specific condition for this state and any state fulfills our requirement of the algorithm as long as the output at the primary register is . The subscripts and indicate the primary and secondary registers however we might leave them out in the cases where it is unambiguous from the context.
It might not be possible to find such an operator as described in (43) because of the assumption that the output state after applying the operator is separable and not entangled. In general, the final state can be entangled therefore we should model the operation of as
In this case, we are looking for an operator that results into a final state with the requirement that
where the operator traces over the secondary register and calculates the density matrix describing the primary register after the operation of .
In this case, although the final state of the registers as a whole might be entangled, we are interested in the primary register being in the state as in (44). Therefore the operator we search for still solves the problem if the final density matrix of the primary register is in our desired state.
Note that this generalized modeling also includes the first case because if the final is non-entangled, we can again write
and we will have
In our derivations, we reserve the possibility of the final state not being exactly equal to , and that is why we have an approximation sign instead of equality in (46). We use the trace distance to quantify this error. The trace distance of two density matrices ρ and σ is defined as
where the norm operator is the trace norm defined as
for any operator .
This means that in our case, we use the trace distance between the output state and the desired state to measure the error
After this preliminary modeling, we recognized that we need to use the density matrix representation to derive the operator because the output state can be entangled and we can only calculate the output of the primary memory after the operator by tracing over the secondary register.
In order to have a consistent mathematical model throughout our derivations, we restate the problem in the most general form using density matrices and use this modeling throughout this work.
4.3Restatement of the problem in the general case¶
Let us now restate the problem after the consideration from the previous section and define all the important parameters for the following derivations.
We start by defining the input states. We assume we have two quantum registers each consisting of qubits. We name the primary register ρ and the secondary register σ. In the most general form, the registers can be in the states
and
where γ and μ represent the basis indices of the -qubit registers.
We assume the initial states of the registers are not entangled and introduce the state describing the initial state of the complete memory consisting of the two registers together as
Our desired final state for the primary register is the state with the following definition
Note how the above definitions are a generalization of the pure state case; because if we assume pure states as inputs, we will have
In this case, we have .
Going back to the general density matrix case, we search for an operator acting on the two registers ρ and σ such that tracing over the second register at the output results in the desired state . Mathematically speaking, The operator should apply the following transformation
where taking the partial trace over the secondary register, we end up with the state
The schematic representation of the operator is shown in Figure 1.
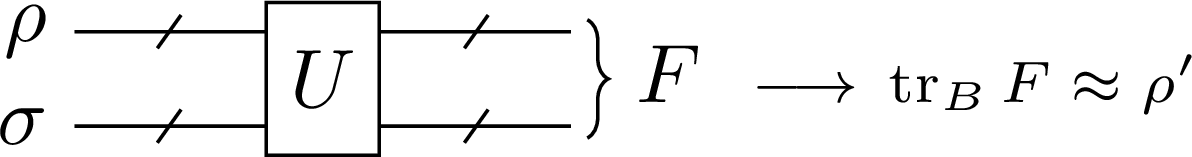
Figure 1:The schematic figure of the partial phase operator
We note that the operator should be independent of the input states ρ and σ, so that applying different phase profiles does not require changing the operator itself. We want to apply different phase profiles using this operator only by changing the input state σ.
In order to analyze the output of the algorithm, we define the subsystems at the output of the primary register as
and at the output of the secondary register as
Then we define the error at the output of the algorithm as the trace distance of the final state of the primary state and the desired state as
Now that we have restated the problem in the general case, we are ready to move forward into the derivation.
In order to provide an overview of the derivation steps, we will briefly discuss the outline of the upcoming derivations in the following and start the derivations afterward.
4.4Outline of the derivations¶
In the following sections, we will take these steps to derive the sample-based phase algorithm described in Section 4.3.
First, we derive the operator that performs the desired transformation described in (57) and (58). As we will see, in order to derive such an operator, we will need to use an approximation. In this approximation, we choose the phase coefficient α in (55) to be small.
As previously mentioned, we use the letter Δ for the phase coefficient in this case to distinguish it from the non-approximated case. The assumption allows us to use Taylor expansions to simplify the derivations. We will find the operator in this case with the condition that it satisfies the (58) up to the first-order approximation in Δ. We call this operator the partial phase operator.
The next step is to find an implementation for the operator previously derived using standard quantum computer gates. It is important to show that the operator can be straightforwardly implemented in practice. We will find an efficient implementation of using CNOT and controlled phase gates.
And finally, we use the partial phase operator to implement an iterative algorithm that applies the phase described in (55) without the approximation of small α. In this algorithm, we repeat the partial phase operator times with small phase steps Δ to apply an arbitrary phase coefficient of
We call this final algorithm the sample-based phase algorithm because it needs copies of the secondary state σ and uses them in iterations to apply the complete phase. We finish the derivations by analyzing the errors of this algorithm as a function of the parameters and Δ.
5The Derivations¶
5.1The partial phase operator¶
Let us start deriving the partial phase operator. The initial state of the memory including both primary and secondary registers is
In several parts of our upcoming derivations, we use the matrix representation of density matrices; therefore it is useful to look at the input states in their matrix form in the computational basis.
We use the unsigned encoding for the basis indices which means the indices are in the range ; however, this choice is only because of the convenience of the notation and the operators we derive solve the problem for general encoding.
We also introduce another tool to simplify our notation. We define in order to simplify the index appearing in the matrix representations. This means the input states are written as
The initial state thus will have the following block matrix form
We keep in mind that we want to find an operator such that
We find using the following steps:
First we simplify the right-hand side of (67) and find a simplified form for the desired state .
Next, we simplify the left-hand side of the equation by choosing an ansatz for and posing several assumptions on the form of it.
In the end, we equate both sides of the equation up to the first-order approximation to find in these assumption conditions.
We also note that in the current steps of the derivations, we are assuming that the phase coefficient we would like to apply (Δ) is small and we use this assumption in the calculations.
Simplifying ¶
Let us investigate the expected output state in more detail. We had
where Δ is a small number such that . This assumption means that we can write
Therefore we have
We define the matrix
which allows us to write
where the approximation is correct up to the first order in Δ. With this, we have simplified the term on the right-hand side of (67). Next, we have to do similarly for the term on the left-hand side.
Before continuing the derivations, let us have a look at the matrix representation in the computational basis.
Simplifying ¶
In order to simplify the term , we take the following steps
First, we suggest an ansatz for .
Next, we simplify the term using the ansatz and the assumption of .
Finally, we trace over the secondary register by calculating . We will end up with a simplified approximated term which we can use to equate with (72) to find .
Let us start with the ansatz. We propose to have the form of an exponential of a Hermitian operator as
where is Hermitian () and has the property of . The motivation for using this ansatz comes from deriving the solution for special cases such as when the registers only have one qubit (). Finding the exact solution for these simpler cases is more straightforward and will lead to guessing such ansatz for the general case since the special case solutions also have such properties. We will see how using this form will simplify the derivations and will enable us to find an operator that satisfies our conditions.
We note that using these assumptions, we have
In order to simplify , we use the assumption of small Δ and write
and similarly,
We can then use this simplified form of to write
where the approximation is correct up to the first order in Δ.
At this point, we have simplified the term using the ansatz and the Δ approximation. We have in mind that we wanted to find such that it satisfies (67). This means that we need to trace over the second register in (78) and find such that the traced-over density matrix is equal to the density matrix in (72).
Tracing over the secondary register, we have
where is defined as
It is not straightforward to further simplify this equation unless we propose several assumptions for . We have in mind that both and are matrices that act on a memory consisting of two -qubit registers, namely . This means that we can represent as a block matrix of the form
where each is a matrix with the dimension of .
For the first simplifying assumption, we choose to be block diagonal which means that only the block matrices at the diagonal locations are non-zero. Applying this assumption, will have the form
This will allow us to calculate the terms and in (80). Before calculating the terms, we note that because of the Hermiticity of and the property of , the block diagonal form we imposed on will result in the following relations for the sub-matrices .
which means are Hermitian and
We can describe the block diagonal form of algebraically as
Using this equation, we can calculate
The block matrix representation of this term is
Tracing over the second register, we will have
where is defined as is the expected value of the operator on the state σ.
And we can also write the algebraic equation for the trace operation as
To better understand this equation, we can compare it to the initial state
and see that the density matrix elements are modified by factors of based on the state of the secondary register σ. We will use this feature to apply the desired phase to the initial state ρ.
In the next step, we have to similarly calculate the term to completely simplify the matrix in (80).
We again write the block matrix as
This allows us to calculate
When we take the trace over the second register, we can write
If we have a look at the second term and compare it to the first term from (88), we can see that the expected values appear at different locations
Having the individual terms calculated, we can simplify the matrix in (80) as
which will have the matrix form of
Now that we have calculated the matrix, we have finally simplified the term on the left-hand side of (67). We had previously showed in (79) that
We can see that the matrix has a form very similar to the previously calculated matrix ((73)) on the right-hand side of (67).
Next, we have to use the results of these derivations to construct the operator and thus find the partial phase operator .
Finding ¶
To review the previous derivations, we wanted to simplify the equation (67) as
by calculating the terms on both sides of the equation using our imposed conditions and approximations.
The results of the calculations from the previous section were, for the right-hand side,
and for the left-hand side,
where and were
and
Our goal in this step is to find the operators such that the equality in (98) holds. When we find these operators, we will be able to construct the operator , which in turn means that we have derived the partial phase operator
We had assumed Δ is small so that we can neglect and higher powers of Δ. This means we only equate both sides of (98) up to the first-order approximation.
In order for (98) to hold, we must have
Also from the equations for the operators and , the above equation for the matrices corresponds to the equation
for all indices γ and μ. Now, we have to find such that this equation holds.
In general, every operator can be represented as an Hermitian matrix. We also assumed they have the property of . We can label the elements of the matrix in the -th row and the -th column as and write the matrix down as
noting that the γ in the terms is not an exponent and it indicates that the element corresponds to the matrix .
We can take the first step for finding the elements by realizing that in (105), there are no off-diagonal elements of the input state σ and only diagonal elements appear in the equation.
This means that we can assume all the non-diagonal elements of are zero
so that no term (where ) will appear in the expected values .
This means that we can simplify as
This allows us to write
In the next step of finding the matrices, we should recall that they were Hermitian and had the property of . The Hermiticity forces the diagonal elements to be real. And the property means that we must have
for all indices .
The relation in (110) does not allow the diagonal elements to be zero. Therefore, we cannot choose them as such, to have which would satisfy (105) straightforwardly. Instead, the elements can only be 1 or -1 because they should be real and satisfy (110).
One way to satisfy (105) and fulfill the above conditions is to choose the elements to be equal to -1 in all -th diagonal locations except for the location where we choose the element to be 1. In other words, we choose the elements as
For example, the matrix representations of and will be
We can see that with this assumption, we will have
where for the last equality we used the fact that σ is a density matrix therefore the sum of its diagonal elements is equal to 1
We can immediately check that this solution satisfies (105) as
With this, the derivation of the operator is complete and we will move on to calculating the partial phase operator ; however, let us first briefly review a summary of the derivations so far to prepare for the following sections.
Summary of the results of deriving ¶
We wanted to find the operator such that
We proposed the operator to have the form of
Furthermore, we assumed Δ is small and solved (116) for using the above operator.
This resulted in constructing as a diagonal matrix with the block-diagonal form of
where are diagonal matrices with -1 on all diagonal locations except for the γ-th location where the diagonal element is 1.
Because we constructed with the condition to satisfy (116), the operator corresponding to is the partial phase operator that we were searching for, meaning that it transforms
to
for small Δ.
However, it is still useful to find the operator itself based on these results and we have to show that it is possible to efficiently implement it in the next sections.
Deriving ¶
Now that we have derived the operator, we should derive an explicit form for . In this section, we put the operator derived in the previous sections in the definition of to find it explicitly.
We recall that was given as
As we will see, corresponds to a simple operator. In order to find , we first recall that had the property of . Using this property, we can expand as
We can see from (123) that because and both have diagonal forms in the computational basis, the operator will also have a diagonal form as
where are -dimensional and diagonal matrices.
The diagonal elements of the matrix are either 1 or -1 and the diagonal elements of are all equal to 1. Thus, using (123), we realize that the diagonal elements of the sub-matrices will be either
or
based on the diagonal elements of the matrices.
Using this correspondence, we can see that the form of the matrix is identical to with the difference that every diagonal element 1 in the operator transforms to in , and every -1 transforms to .
We can for example write the matrix representations of and as
With this, we have derived the explicit form of the operator .
This section marks the end of deriving the partial phase operator . In the upcoming section, we will find an implementation of this operator for quantum computers. Later, we will show how we can use this operator iteratively to overcome the limitation of the small phase coefficient Δ as one of our assumptions in the current derivations.
5.2The implementation of the partial phase operator ¶
Previously, we derived a simple form for the operator , but we still have not shown how it can actually be implemented using standard quantum gates. We will now find an implementation by analyzing the action of on the basis states and trying to find quantum gates that perform the corresponding action. To do this analysis, we must revisit our definitions of the computational basis states of our quantum memory and their correspondence to the pattern of the eigenvalues of .
We have defined our quantum memory as a combination of a primary register in the first position and a secondary register in the second. Each register has qubits and we can define the basis states of the memory as a whole as
where γ and μ are respectively the basis indices of the primary and secondary registers. Each register has basis states therefore the whole memory will have basis states.
We showed that has a diagonal form in the computational basis ((124) and (127)). This means that all the computational basis states are eigenstates of
We also derived that the diagonal elements of are either or . It means that the eigenvalues in (129) are correspondingly either or . Our goal is to derive an explicit equation for the eigenvalues .
We can start by writing the algebraic form of from (124) as
Now applying the operator on the basis states, we will have
Now we recall that was a diagonal matrix with as all of its diagonal elements except for the γ-th diagonal element where the value was ((127)). And considering the representation of the computational basis states as
the term is evaluated as
This means that we can write
In other words, given the basis states of the two registers, and , the operator (ignoring the overall phase) applies a Δ phase if the two registers are in the same basis state and does nothing otherwise.
Now that we have understood the action of the operator on the basis states, we shall search for an efficient implementation of it using standard quantum gates.
As previously derived, the operator applies a phase with the condition that both of the registers are in the same basis state. We write this condition as
However, we must note that each basis state actually consists of qubits as
where each can be in one of its basis states or .
This means that the equality of the basis indices γ and μ is one-to-one related to the equality of the individual qubits.
Having decomposed the basis states of the registers to their qubits, let us derive an efficient implementation of the operator acting on individual qubits.
We can start by defining the equality flag bits for each corresponding qubits as
The flags show whether the -th qubits of the two registers (primary and secondary) are in the same state or not.
We need to first calculate these flags in our quantum computer and then apply the phase Δ to the registers if all of the flag bits are equal to 1. It is important to note that the operations should be done using quantum unitary gates without involving any measurement because measurement will force the wavefunction to collapse and therefore the initial state will be lost.
In our implementation, we temporarily use one of the registers to store the calculated flag bits and recover the original state after the operation. In this way, we will not need to introduce an ancilla register to store the flags.
We first recognize that the flags can be written as a logical function as
where is the XOR operator and the bar over is the logical NOT operator. As we will explain in what follows, the flag bits can be computed using CNOT gates on a quantum computer using this logical function.
The standard CNOT gate is defined as acting on two qubits called control and target qubits, and it flips the target qubit only if the control qubit is in the state. This action can be written as
where is the control and is the target qubit, and and can be zero or one . Note that .
In this case, the CNOT gate performs a not operation if the control qubit is . We can denote this type of CNOT operator as in order to contrast it with the other type we will introduce shortly. We have shown this operator in the circuit representation in Figure 2 where the dot on the state indicates that it is the control qubit.
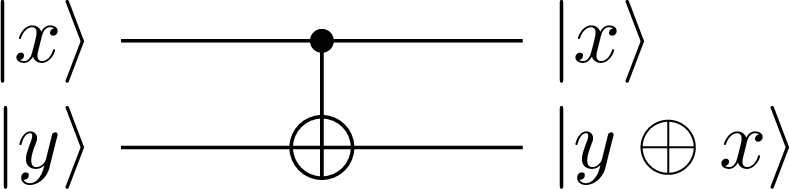
Figure 2:The CNOT operator with 1 as its control state ()
There is also a second type of CNOT operator that flips the target qubit if the control qubit is in the state . We can denote this operator as with the following definition
This operator is drawn in Figure 3, where the non-filled dot indicates that the control state is 0.
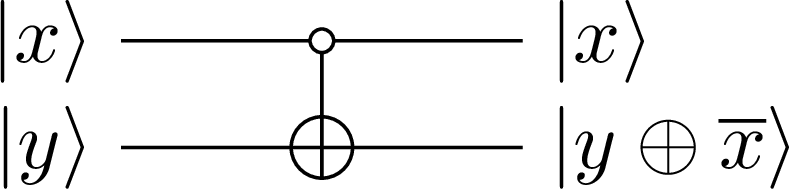
Figure 3:The CNOT operator with 0 as its control state ()
It is very straightforward to show that the two types of CNOT operators correspond to each other by applying Pauli operators on the control qubit as in Figure 4.
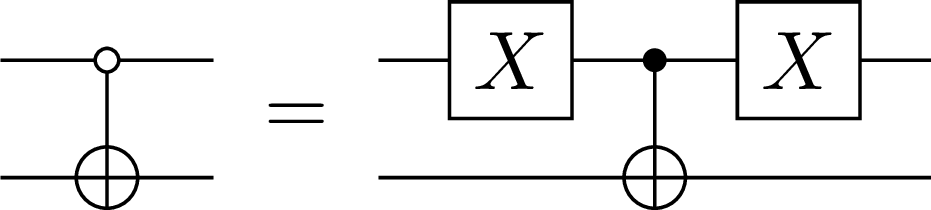
Figure 4:The equivalence of the CNOT operators with different control states
After introducing the operator, we can see that it exactly performs the transformation we need to calculate the flag bits from (139). Each flag bit can be calculated in the qubits of the primary memory as
The calculation of the flags is demonstrated in Figure 5 for the case of 3-qubit registers, where and are respectively the primary and secondary registers.
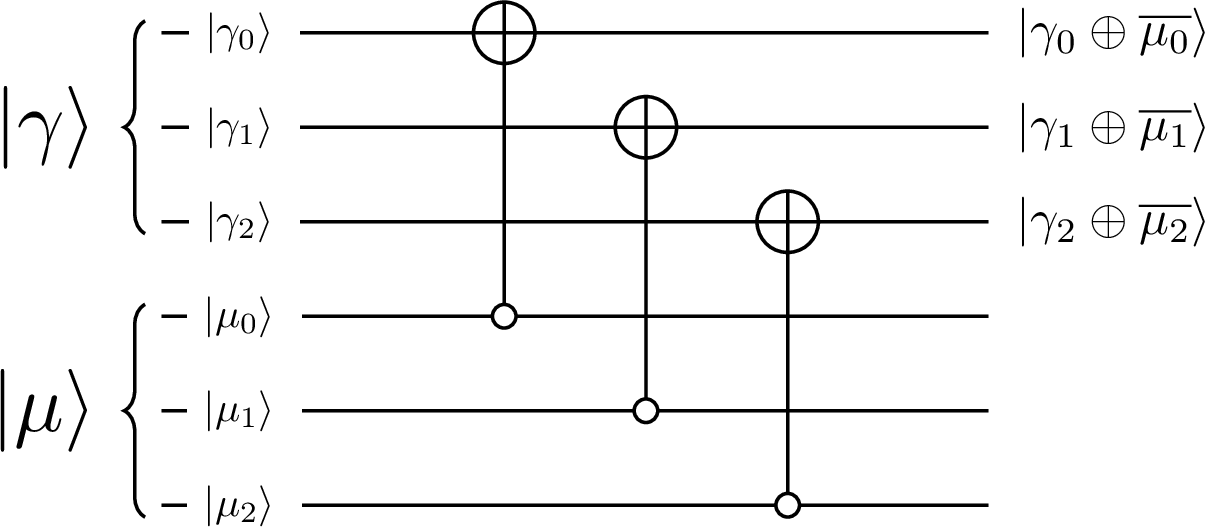
Figure 5:The preliminary flag bit calculation for the partial phase operator, for the case of
Now, we only have to apply a phase term to the state if all the qubits are in the state. This is exactly the action of the controlled phase operators with multiple control qubits; they apply a phase if all the input qubits are in the state . We just need to apply this multi-qubit phase operator with the phase value of Δ on all of the calculated flag qubits. This is drawn in Figure 6 for the case of the 3-qubit register example, where is a phase operator with the phase value of Δ, defined as
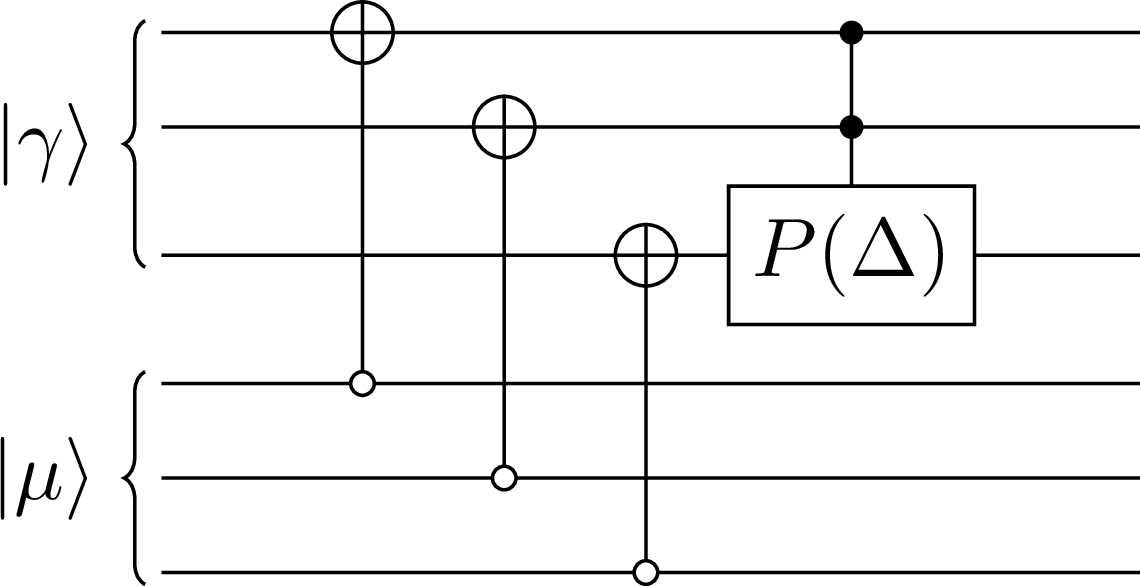
Figure 6:The circuit that applies the phase Δ if the input registers are in the same basis state, for the case of
After this step, the desired phase Δ is applied to the memory if the input registers and were in the same basis state. However, the circuit in Figure 6 is not the complete partial phase operator because the primary register was transformed by the flag bit calculator circuit. In order to recover the primary state, the only thing we have to do is to re-apply the same CNOT operators to un-compute the previous calculation. You can see the complete implementation of the partial phase operator in Figure 7.
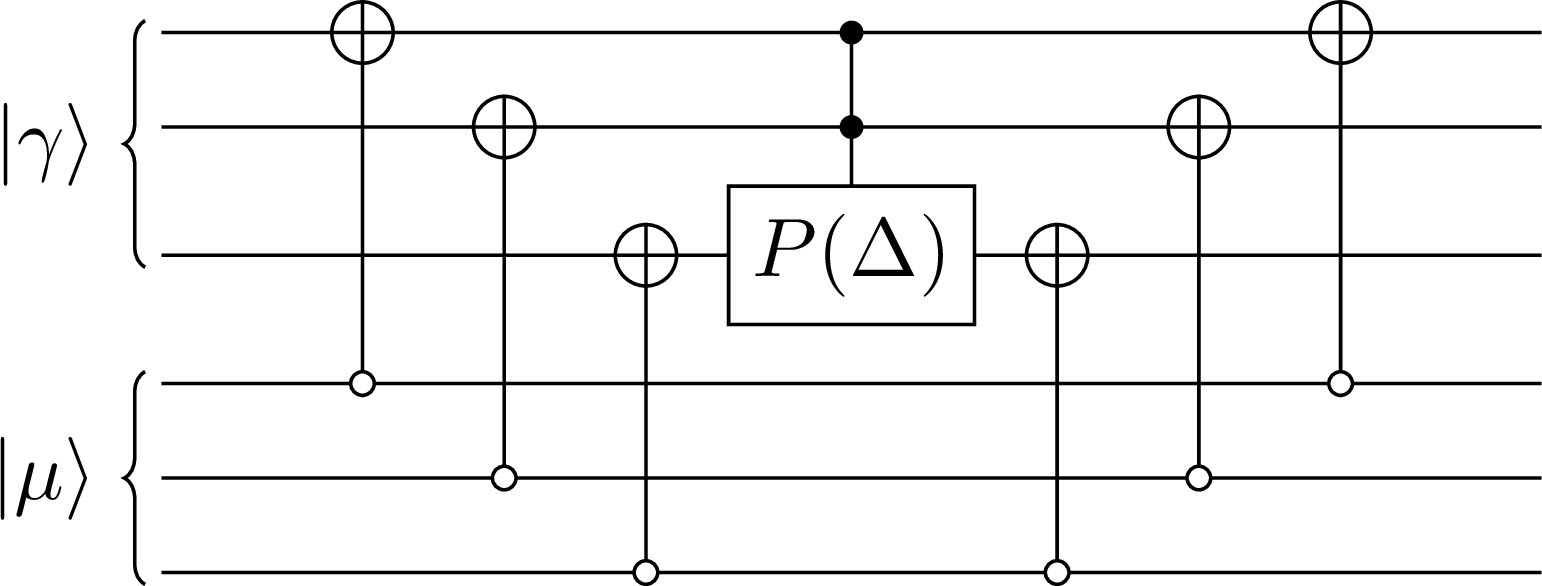
Figure 7:The implementation of the partial phase operator in the case of 3-qubit input registers
The final recovery of the primary state is possible because the phase gate does not modify the index of the state of the register and only applies a phase term to it. We also used the fact that for any logical bit , we have
and
After the application of the phase operator, the state of each of the qubits of the primary register is ; therefore, using the definition of the operator, we have
This means that each CNOT operator will recover the original state of the corresponding qubit and by applying the operation on all the qubits, we will completely retrieve the initial state of the primary register .
This section marks the end of deriving the partial phase operator. In the previous sections, we mathematically constructed the operator which applies the desired phase transformation on the input state, and in this section, we presented an implementation of that operator.
We can see that the gate complexity of the partial phase operator is
because it needs CNOT gates and the phase operator can also be implemented using gates Nielsen & Chuang (2010).
We also note that we did not use any ancilla qubit in this implementation of the operator, because we efficiently used the existing qubits to temporarily calculate and store the intermediary variables and we were able to recover the original qubits after the operations.
One very important feature of the operator is that it is agnostic about the input states therefore we do not need to change it to apply different phase profiles to the primary register. In this algorithm, not only the state that receives the phase is encoded in a quantum register as the input, but also the phase itself is stored as a part of the quantum algorithm in a secondary register.
Therefore, the algorithm reduces the problem of applying different phase profiles
to a quantum register to the problem of being able to initialize a secondary register to the state that corresponds to a desired profile as
After completing the derivation of the partial phase operator, we have to overcome the limitation introduced by assuming . Throughout the derivations, we assumed the phase we want to apply is of the form
where Δ is a small real number. But in general, we would like to apply any phase
for any real number α.
The goal in the next section is to use the partial phase operator to derive an algorithm that applies the phase profile with arbitrary phase coefficient α.
5.3The iterative phase algorithm¶
In the previous section, we derived an operator that (for small Δ) can transform
to
However, our goal in this work was not to only apply small phase coefficients Δ but we wanted to apply arbitrary phase coefficients α as
In order to achieve that, we propose an algorithm that iteratively applies the previous partial phase operator times to the primary memory to apply the phase with a desired phase coefficient. This will allow us to apply arbitrary phase coefficients α even though the phase step Δ should be small for the individual partial phase operators to work.
In this approach, we need multiple copies of the secondary register σ. Let us assume we have copies of σ. Note that having multiple copies of σ is possible and it will not contradict the no-cloning theorem because we completely know the σ state since we choose it to correspond to a specific and predetermined phase profile. Therefore, we can initialize quantum registers to the state σ with our initializers as many times as necessary.
In this section, we will show that if we repeat the partial phase operator times where each operator applies the phase step of Δ using the copies of σ, the overall effective phase coefficient of will be applied to the primary register. Furthermore, we calculate the error of this algorithm as a function of the parameters and Δ. As we will see, the error δ (defined as the trace distance of the output and the desired states) is
This error analysis allows us to find out how many copies of σ we need to apply the desired phase coefficient α while achieving a desired final accuracy δ.
We will take the following steps for the derivations in this section
We properly model the iterative algorithm, calculate the desired state and define the error in terms of the input parameters.
Then, we go through the recursive calculations at each iteration of the algorithm and derive the output state of the algorithm as a function of ρ, σ, , and Δ.
We end this section by analyzing the final error based on the calculations from the previous steps and discussing the implications of changing the input parameters on the final error.
Modeling and error proposal¶
Assume we have copies of the state σ. We start with our primary register ρ and the secondary registers σ which means we can describe the state of the initial memory as
The algorithm applies the partial phase operator derived in the previous section using the primary register and one of the copies of σ as input states at each iteration step.
We model the iterations as follows. We regard the initial state of the primary register ρ as the 0-th step and denote it as . This means before running the algorithm, we have
We use the index to indicate the value of a parameter after the -th iteration.
In the first iteration, we use one of the secondary states σ and apply the partial phase operator with the phase step of Δ as
After this step, similar to the original partial phase operator, we discard the secondary register to work with the new state of the primary register as
The state is the state of the primary register after the first iteration. At the next iteration, we use the new state of the primary register and another copy of σ. We repeat the partial phase operation using these states to calculate the state of the primary register after the second iteration as
Similarly, we repeat this operation times to calculate . The state is the final state at the output of the iterative phase algorithm. We note that at each iteration, we have the recursive formula of
where is the state of the primary register after iterations. This is the formula we will evaluate in terms of the initial state and the other parameters that will enable us to analyze the final error.
We define the error as the trace distance error between the final state and the desired state . The trace distance was defined in the introduction sections in (49). Thus, the error is given as
We are in particular interested in the error as a function of the parameter to see if we can decrease the error by increasing the number of iterations for a fixed phase coefficient α.
The desired state is also defined as
given the initial state was
Recursive calculations¶
Let us start evaluating the recursive formula of the iterations
As the first step, we substitute the definition of the partial phase operator
into (165) to write
Next, we take the partial trace which results into
In order to simplify this equation, let us define
and
and to rewrite the equation as
Next, we will find the matrices and .
Calculating ¶
We recognize that has exactly the form of the matrix from (80) that we calculated in the derivations of . Using the calculations from the previous derivations, we can write
In the later error analysis, we will need to derive an algebraic form for the matrices and . In order to do so, we introduce two matrices defined on the input states ρ and σ which will help in writing down algebraic forms for our matrices.
We define as a matrix derived from σ which has the same diagonal elements as σ but all its off-diagonal elements are zero. Therefore, for the matrix σ as
the matrix will be defined as
It is easy to see that if this operator applies on ρ from left or right, we will respectively have
and
Therefore, we can write
Using the definition of , we can write the matrix from (172) as
which is the form for we will use later for the error analysis. Now we must similarly calculate the matrix .
Calculating ¶
In order to simplify we use the definition of as a block matrix and write
Putting this definition in (170), we will have
Now, considering the form of matrices derived in (111) and (112), one can calculate
Using this lemma, we can write
Simplifying the terms and using the definitions of the and matrices, we can finally write
where is the anti-commutator defined as
An important note is that the matrix does not change at each iteration meaning that we have
because the diagonal elements of ρ do not change after applying the partial phase operator at each iteration (see (153)) and that is why we can leave out the index of in (183).
Writing down the recursion using and ¶
Using the calculated and , we can rewrite (171) as
which simplifies into
Now, we apply a Taylor expansion on the and functions for small Δ resulting into
Evaluating the recursive formula¶
The next step is to evaluate the recursive formula in (188) to derive a formula for as a function of the initial state .
Let us start by calculating the next recursion by putting the equivalent of as a function of in (188). By putting the term in the equation and ignoring the terms including and higher powers of Δ, we will have
Simplifying the terms, we will have
At this point, we have derived a formula for as a function of in (190). We have to repeat calculating these recursive steps until we reach a formula for as a function of .
If we continue the calculations for recursive steps, we can see that as a function of will be
for any positive integer number . We can check that this equation matches the manual calculations we did previously for and .
Using (191), we can find as a function of by choosing and writing
This means that the final state after applying partial phase operations with all the copies () will be
This equation describes the state of the primary register after iterations () up to the second order approximation in Δ as a function of the number of iterations , the initial state ρ, the secondary state σ, and the phase step of each iteration Δ.
Next, we have to compare this output state with the desired final state.
The desired state¶
The initial state was
and the desired state was
We can use Taylor expansion to write
The partial phase operator was derived with the condition that it was correct up to the first-order approximation. This means we expect the calculations to be correct up to the first order therefore we keep the terms up to the second order in Δ to be able to analyze the accuracy.
We can further write
Now using the definition of the matrix, we can rewrite the equation as
This is the desired state Taylor-expanded up to the second-order approximation in α. We can see similar terms in this equation and the state at the output we calculated in (193). Next, we analyze these two states to calculate the error of the algorithm.
Error analysis¶
We can see that if we choose and substitute it in (198) of the desired state, we will have
And comparing this state with the output of the iterative algorithm from (193), we can see that
This means that for the trace distance error, we have
With this, we have proved that the error is
This means that if we choose the maximum tolerable error of the final output of the algorithm to be δ and would like to apply the phase profile to the primary register ρ, we need to iteratively apply the partial phase operator
times on the primary register using copies of the state σ where each phase step is equal to
This final remark ends the error analysis section. Now we have a complete understanding of the partial phase operator and its use in the sample-based phase algorithm.
We also note that the partial phase operator we derived previously corresponds to the case of one repetition in the iterative phase algorithm, and in this case, the trace distance error will be which confirms our previous derivations where we derived to be accurate for small Δ if is negligible.
In the next section, we will put our derivations to test by implementing the algorithm on a computer and verifying the error dependencies derived in this section. But before moving on to the implementations, let us briefly discuss what we can infer about the fidelity based on this error analysis.
Fidelity analysis¶
The fidelity analysis is important to us because we will use it in the implementation in the next section to verify our derivations.
In the error analysis, we used the trace distance error
as a measure for the similarity of the output and the desired states. If δ is zero, it means that the output state is identical to the expected state.
We can also use another measure for this similarity which is the quantum fidelity Wilde (2013) of the two states
where the fidelity of states ρ and σ is defined as
Using this definition, the fidelity equal to one corresponds to the two states being identical.
It is difficult to calculate the fidelity using this formula in the general case when both input states are mixed states. Yet, there is a general inequality relation between the trace distance and the fidelity of two states as
In the case when at least one of the states ρ or σ is pure, the fidelity formula reduces to a simplified equation as
and one of the inequality bounds becomes tighter as
As we will see in the implementation section, we can use this simplified case because usually, we would like to apply phases to a particular state which is initially a pure state
This means that the ideal expected state after the application of the phase will also be a pure state
Therefore, the fidelity of the output of the phase algorithm and the expected state will have the simple form of
And by combining the inequality in (210) and the trace distance calculated in (201), we can in this case write
which means
We will see in the implementation section that there is a quantum subroutine that can directly calculate the fidelity of two states inside the quantum computer when one of the states is pure.
The ideal result for the phase algorithm is if the final output state is identical to the desired state; this case corresponds to the fidelity being equal to one. (215) shows how we can bring the fidelity close to 1 by increasing the repetition number for a fixed phase coefficient α using the relation
We will use this fidelity analysis to verify our algorithm in the implementation section.
6Simulation and verification¶
After deriving the phase algorithm and discussing its accuracy in the previous sections, we progress to implementing it and analyzing its error dependency in this section. We use the Python programming language Van Rossum & Drake (2009) and the Qiskit library A-v et al. (2021) to implement and run the algorithm. We use the quantum computer simulator provided by the library to simulate running the algorithm on a quantum computer.
We will start by defining a scheme for the verification procedure. Later, we run the scheme using different initial parameters such as the number of iterations and the partial phase step Δ and analyze the results in the following section. We will show that the errors behave as expected according to the derivations in the previous sections.
6.1Implementation scheme¶
Let us start by reviewing the important parameters for the implementation:
: The initial state of the primary register.
: The phase profile we would like to apply consisting of a normalized profile and a phase coefficient α
Δ: The phase step that is applied at each iteration using the partial phase operator.
: The number of iterations which is related to the other parameters as
Considering these parameters, we take the following steps to implement a verification procedure. We chose the quantum registers of the primary and the secondary states to consist of qubits for this demonstration, corresponding to number of sample points stored in each register.
Primary state: We choose a superposition of all basis states as the initial state of the primary register as
and we initialize the primary register to this state at the beginning of the algorithm. Any other state could have been chosen as the initial state but we chose this homogeneous state in order to have all the basis states in the superposition allowing us to characterize the phase algorithm acting on all the basis states.
Secondary states: Next, we pick a normalized phase profile to apply to the primary register. We will use as the state of the secondary register in the phase algorithm. The aim is to use this phase profile along with different numbers of iterations and phase steps Δ to apply an overall phase to the primary register according to the relation
This means that for different cases of , we need to prepare copies of the state
for the partial phase operators.
For this demonstration, we choose to be
Using this state as the secondary states, we expect the output state of the primary register to be
for each case of and Δ,
The phase algorithm: Now that we have prepared all the quantum registers, we will iteratively use each of the copies of and apply the partial phase operator on the primary register using the states. We call the final state of the primary register at the output of this algorithm and we expect it to be equal to .
Fidelity analysis: And finally in order to analyze the accuracy of the algorithm, we use the fidelity of and as a measure for the accuracy.
As discussed in the derivations section, because the desired state is a pure state, we expect the fidelity to behave as
for different cases of and Δ, and the formula for the fidelity to have a simple form as
In order to calculate the fidelity, we use a subroutine that directly acts on the output register to estimate the fidelity using the quantum computer.
It is important to note that because the phase algorithm only changes the phases of the initial state, directly measuring the output state in the computational basis and sampling the corresponding probability amplitudes will not reveal information about the applied phases. That is why we use such a subroutine to calculate the fidelity directly using the quantum computer, instead of measuring the output state and classically calculating the fidelity afterwards using its formula.
Another possibility was to use the quantum phase estimation (QPE) algorithm Kitaev (1995)Nielsen & Chuang (2010) to estimate the applied phases but it is not practical because one has to run QPE for each basis state to estimate the individual phase terms applied to the corresponding basis.
The subroutine Miszczak et al. (2009) consists of an ancilla qubit and two input registers that have the same number of qubits. Let us call the ancilla qubit and the input registers and . The subroutine is plotted in Figure 8.
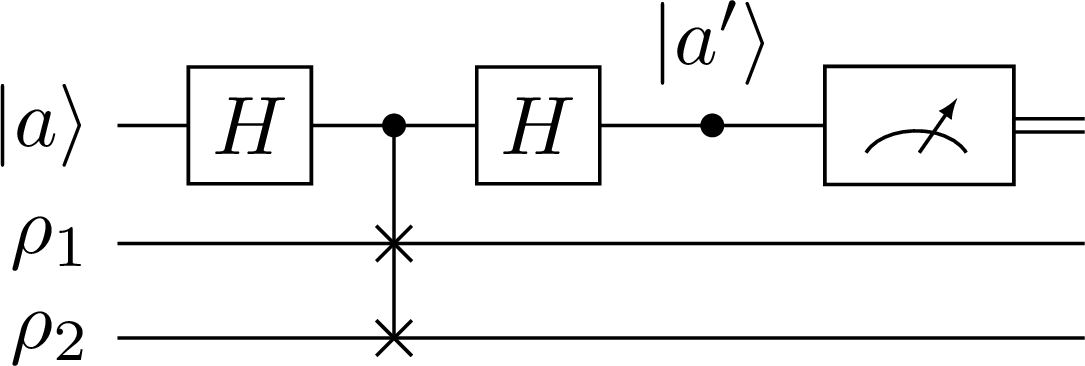
Figure 8:A quantum subroutine calculating the overlap of two states .
It is straightforward to show that the expected value of the Pauli- operator on the ancilla qubit at the output is equal to the overlap of the input states as
Therefore, we can feed in the output of the phase algorithm as one of the inputs and initialize the second register in the expected state ; then using this subroutine, we can calculate the fidelity as
Note that the overlap is equal to the fidelity in this case only because one of the input states is pure where
We also note that the expected value of the operator is nothing but the difference of the probabilities of measuring the ancilla qubit in the state or
Statistical considerations: Each time we carry on the steps 1 to 4 and measure the ancilla qubit of the fidelity calculator subroutine, we will measure the ancilla qubit being in one of the states or . In order to estimate the fidelity, we need to repeat the steps several times to have an accurate estimation of . We call the number of times we repeat the steps for estimating a specific “the number of shots” and denote it as .
After each case of running the scheme, we will end up with an estimation for the fidelity for a specific and Δ, and if we repeat that for different and Δ, we will have an estimation of the fidelities as a function of the parameters as
However, because we are also interested in the statistical errors of the calculations, we will repeat the calculations for each several times in order to calculate the average and standard deviation for each case and to be able to calculate the corresponding error bars and ensure reproducibility. We call this repetition number .
The preceding verification procedure is schematically shown in Figure 9.
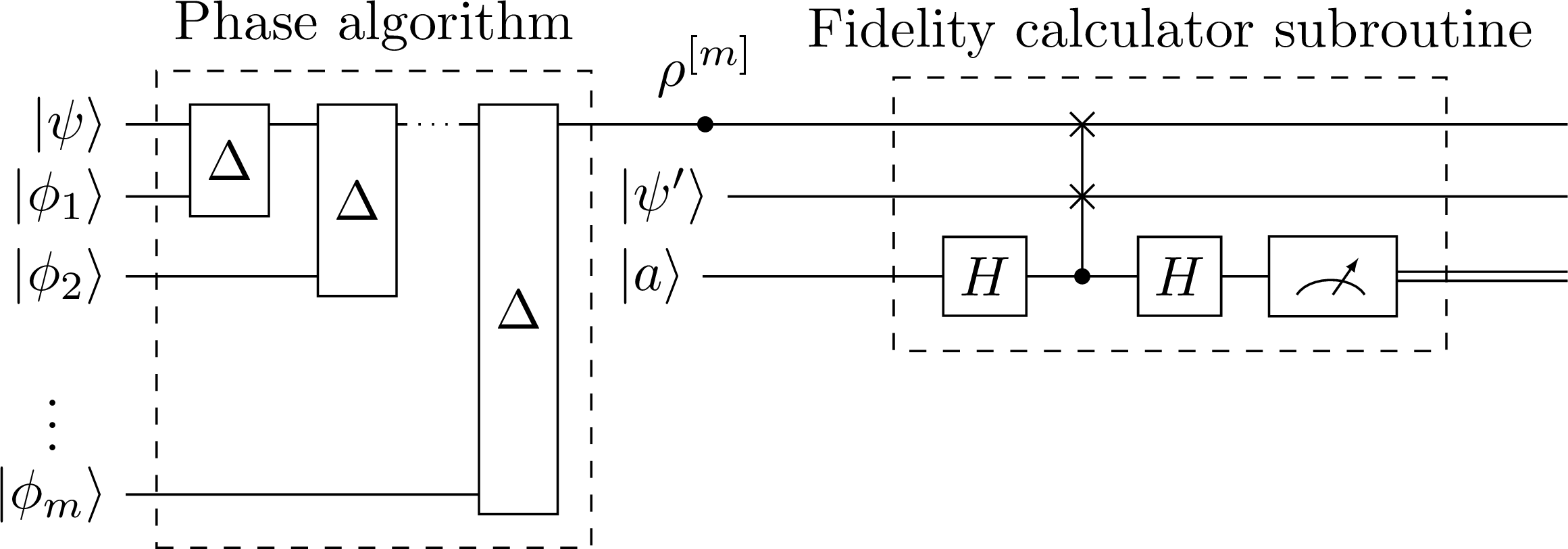
Figure 9:The schematic figure of the verification procedure
We run the verification for the cases of the phase steps
and the number of repetitions
In the end, we will end up with an estimation of the fidelity for the above-mentioned parameters and verify if it demonstrates the expected functionality we derived in our calculations
6.2Analysis of the results¶
Let us provide and discuss the results of the simulations.
For the estimation of the fidelity in each case, we repeated the algorithm for number of shots, and in order to analyze the statistics, we calculated each fidelity times.
We can see the results in Figure 10 and Figure 11. Figure 10 plots the fidelity as a function of (the number of iterations) for the cases of different Δ (phase step of the partial phase operators); and Figure 11 plots the fidelity as a function of Δ, for the cases of different iterations . The dashed lines in Figure 10 and Figure 11 are respectively, linear and quadratic regressions of the measured fidelities.
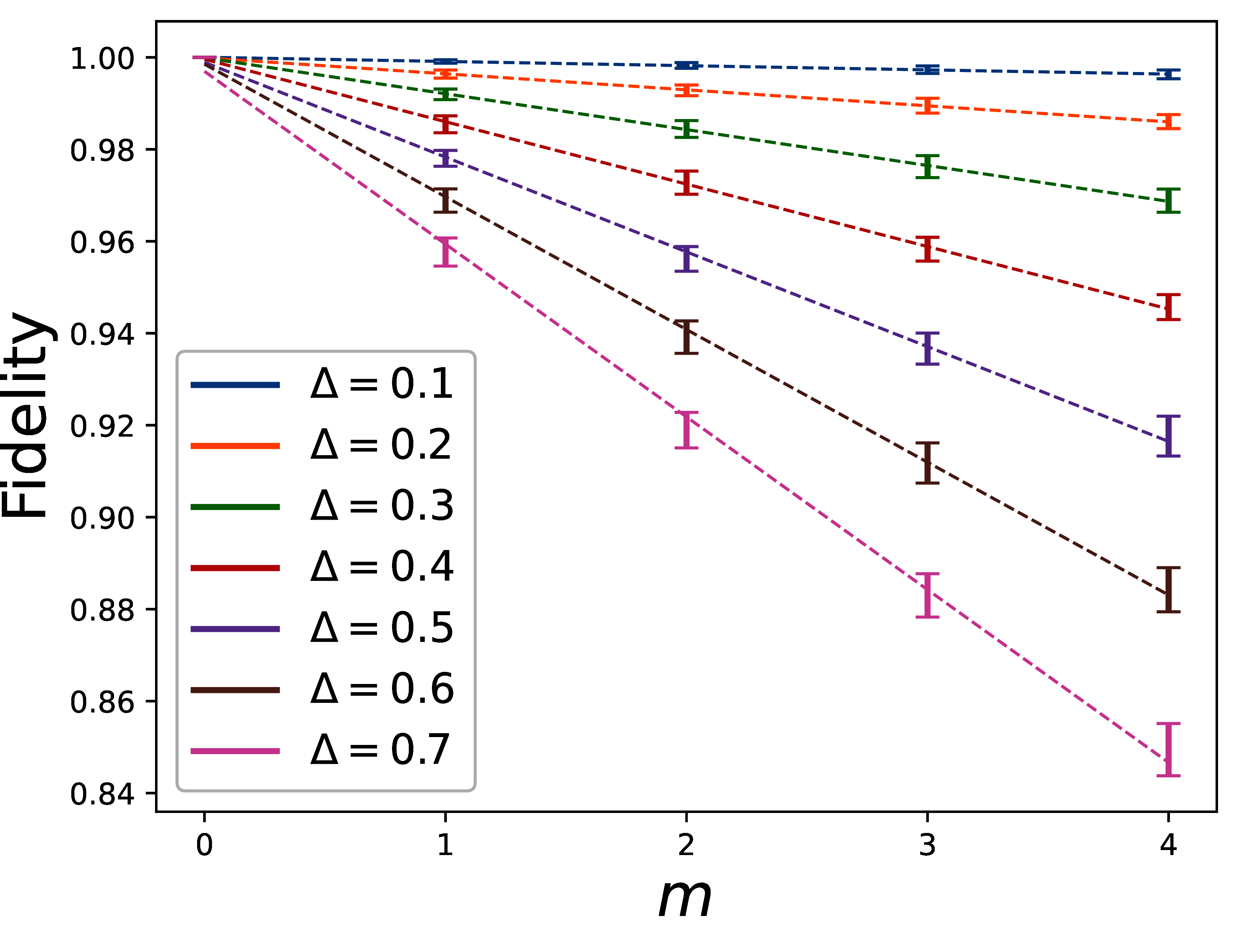
Figure 10:The error bar plot of the measured fidelity at the output of the phase algorithm as a function of for different phase steps Δ and the linear regression lines.
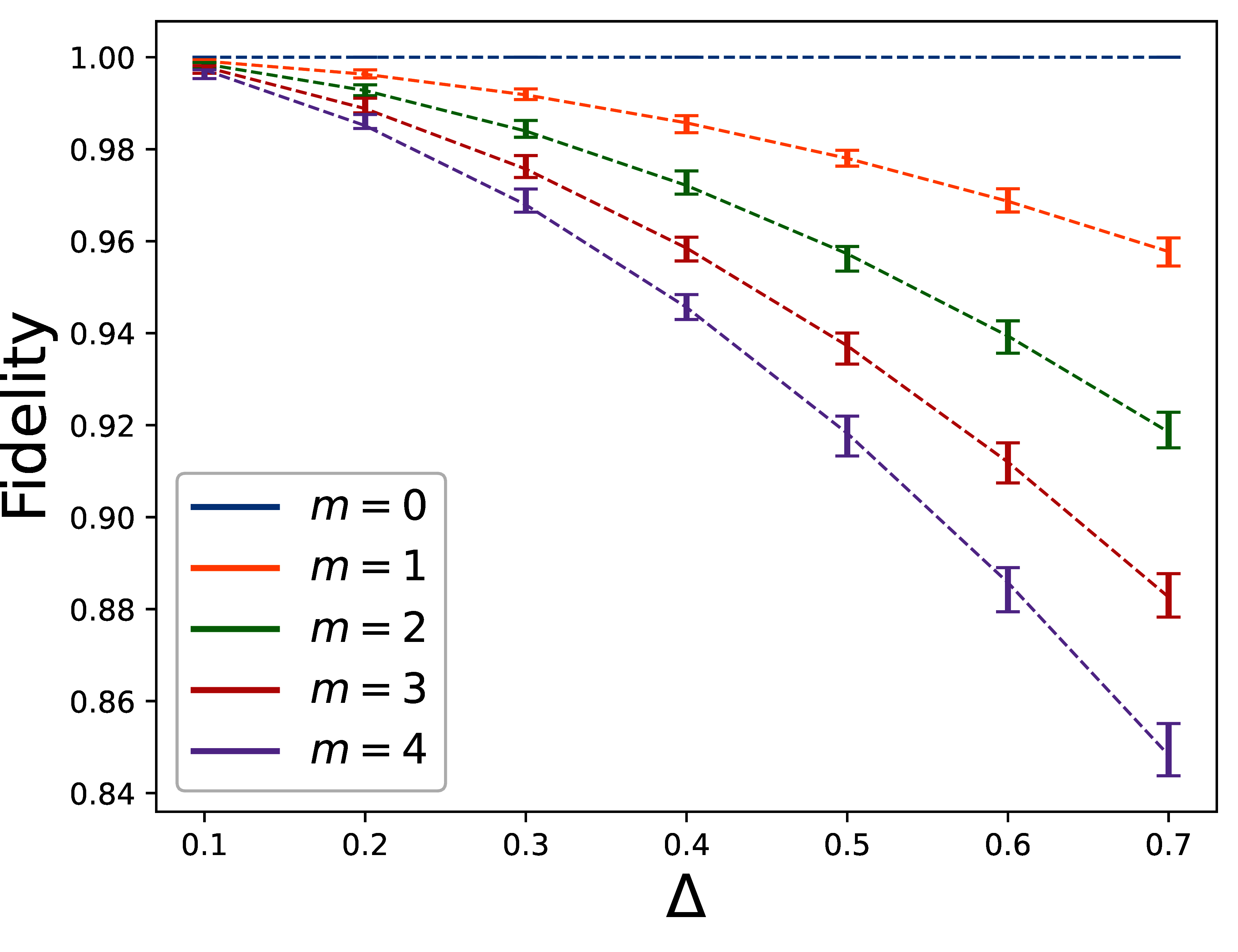
Figure 11:The error bar plot of the measured fidelity at the output of the phase algorithm as a function of Δ for different number of iterations and the quadratic regression lines.
As we can see, the results confirm the linear and quadratic behaviors of the fidelity as a function of the parameters and Δ as expected in (234). Using the regressions, we can calculate the proportionality coefficient in (234) to be
for the range of and Δ we used in our case, where β is
Using this verification scheme, we managed to characterize the accuracy of the phase algorithm using quantum fidelity. However, we can also analyze the output state of the algorithm in terms of wavefunctions instead of calculating the fidelity using the fidelity calculator subroutine.
Analyzing the wavefunctions¶
We know that the output of the phase algorithm is, in general, described as a density matrix . Therefore, we cannot represent it using just a single wavefunction. What we can do instead is to diagonalize this Hermitian matrix in its orthonormal basis as
where are the eigenvalues and correspond to the probability of being in the state . We also have .
The generally high fidelity in our previous simulations suggests that the output state is close to the desired state . It means we expect one of the probabilities to be close to one and most of the others to be close to zero; and therefore, just one of the states to significantly contribute to , and we expect this state to be close to the desired state . We can therefore choose the highest probability and call its corresponding state from the diagonalization, then we can use this state to approximately represent the output density matrix as long as the probability is close to one.
This allows us to compare the wavefunction of the state to the expected wavefunction of by plotting them in a figure. In the following, we will present the results of such simulations.
For this section, we choose a fixed phase coefficient and realize it in five cases
According to the previous error analysis, we expect the accuracy of the phase algorithm to decrease by decreasing the number of iterations for a fixed α.
For each case, we run the phase algorithm as previously described in the scheme but only take steps 1 to 3. Then, instead of performing the fidelity analysis, we extract the density matrix at the output from the Qiskit simulation, diagonalize it, and plot the phase and the amplitude of the wavefunction of the highest contributing state. We note that this simple extraction of the matrix is possible only because we are using the quantum computer simulator of Qiskit, whereas, in a real quantum computer, one has to perform state tomography to estimate the density matrix. We also note that there are no statistical considerations involved as we are not sampling the results of measuring an observable but analyzing the results directly using the states.
We can see the results of the simulations in Figure 12 to Figure 16. In each figure, the wavefunction corresponding to the state is plotted along with the desired wavefunction as a reference. In the figures, we have also included the probability , to which the state corresponds in the diagonalization of .
![The comparison of the highest contributing wavefunction \eta(\gamma) to the output state \rho^{[m]} with the expected wavefunction \psi'(\gamma), in the case of m=5, \Delta=0.2.](/build/08.02.2024_10.34.41--b7f58a9acd8be25490ba63b1fa9ea154.png)
Figure 12:The comparison of the highest contributing wavefunction to the output state with the expected wavefunction , in the case of , .
![The comparison of the highest contributing wavefunction \eta(\gamma) to the output state \rho^{[m]} with the expected wavefunction \psi'(\gamma), in the case of m=4, \Delta=0.25.](/build/08.02.2024_10.34.44--37976433b313828828a70c4a38c9b11d.png)
Figure 13:The comparison of the highest contributing wavefunction to the output state with the expected wavefunction , in the case of , .
![The comparison of the highest contributing wavefunction \eta(\gamma) to the output state \rho^{[m]} with the expected wavefunction \psi'(\gamma), in the case of m=3, \Delta=\frac{1}{3}.](/build/08.02.2024_10.34.46--919561d8bdb1b772299debd2ec43f2d3.png)
Figure 14:The comparison of the highest contributing wavefunction to the output state with the expected wavefunction , in the case of , .
![The comparison of the highest contributing wavefunction \eta(\gamma) to the output state \rho^{[m]} with the expected wavefunction \psi'(\gamma), in the case of m=2, \Delta=0.5.](/build/08.02.2024_10.34.47--13c91d28e81659f117cfb6ec68317fa8.png)
Figure 15:The comparison of the highest contributing wavefunction to the output state with the expected wavefunction , in the case of , .
![The comparison of the highest contributing wavefunction \eta(\gamma) to the output state \rho^{[m]} with the expected wavefunction \psi'(\gamma), in the case of m=1, \Delta=1.](/build/08.02.2024_10.34.49--a60e6a937c24aeb27caa04dab9b0df8f.png)
Figure 16:The comparison of the highest contributing wavefunction to the output state with the expected wavefunction , in the case of , .
As we can see in the figures, the wavefunction closely resembles the expected wavefunction in most cases. Only when Δ reaches the higher values of and , the wavefunction significantly deviates from the expected . Comparing the values, we can also see how the density matrix deviates from being a pure state as Δ increases.
This simulation is in agreement with the previous fidelity analysis and allows us to have a look at the output wavefunction itself in the weak sense of the highest contributing eigenstate in the diagonalization of .
With this, we will conclude the verification of the phase algorithm we derived previously in Section 5 and the main body of this thesis report.
7Conclusion¶
In this work, we derived a quantum phase algorithm that receives two input states and is capable of applying phases to one of them based on the state of the other. The algorithm transforms an initial state
to the state which is approximately equal to
given copies of the state
with a final trace distance error of
Assuming the registers are initialized to the input states, the gate complexity of each step of the algorithm is
where is the number of the qubits of the registers.
The important property of this algorithm is that the phase profile that is applied to the primary register is provided to the quantum computer as another state encoded in a quantum register. This property reduces the problem of applying phase profiles to a quantum register to the problem of initialization. As long as we can initialize the phase profile efficiently in a quantum memory, we can apply a corresponding phase to our primary register.
7.1Remarks and limitations¶
We note that for the cases of small phase coefficients , the phase algorithm has an excellent performance both in terms of gate complexity and memory consumption since the error will still be low even using one iteration .
However, the main limitation of the algorithm in its current form is the memory consumption for the cases of large α because of the square dependency in the error. Because the error increases as , if we would like to achieve a constant error while increasing α, we have to also increase the number of samples used in the iterations as .
We can propose several ways to deal with this limitation.
In our discussions in this thesis report, we assumed we wanted to apply phase terms
corresponding to a phase profile , and α was the normalization factor of the phase profile .
First, we realize that global phases do not result in different quantum states. This means that adding a constant real number to will not change the final state of the output of the phase algorithm
We also realize that adding multiple factors of will not change the output state either
because both phase profiles will correspond to the same phase terms ; the factors are integer numbers that can generally be different for different phase terms .
Now combining both of the observations, we recognize that we have the freedom of constructing a phase profile based on the initial desired profile as
and using as the phase profile in the phase algorithm will result in the same output state as in the case of using .
This freedom of choosing the phase profile combined with the fact that phases can always be bounded between will allow us to construct a phase profile for any that in some cases can potentially have smaller definite integral thus a smaller normalization factor
Using the new state and the smaller phase coefficient , we will need less number of iterations compared to the original case of using .
Continuing the previous suggestion, we also note that because of the bounds , there will be an upper limit to the definite integral and thus the phase coefficient α, as we can always limit the phase between these bounds no matter how large the profile is.
Therefore, we can recognize that the squared dependency in is only true for small α and for large α, the error will hit a limit in terms of α dependency. One can investigate this effect in more details to find the exact relation of the error for large α.
7.2Outlook¶
The phase algorithm introduced in this work is useful for many interesting applications. The key concept for making use of this algorithm is to find a way to model a specific problem as a problem of phase transformation. We briefly touched upon possible applications in the introduction of this thesis but will now suggest them as use cases of the phase algorithm worthy of further investigations.
Before discussing the applications, let us look into the relevance of the quantum Fourier transformation (QFT) Nielsen & Chuang (2010). Combining the phase algorithm with the QFT greatly broadens the range of problems solvable by the phase algorithm. Assume we are given a signal , and we have discretize it with a sampling period of and stored the discretized signal in our quantum register as
where . Applying the QFT operator on this register will result in
where is the discrete Fourier spectrum of the signal and .
We note that the QFT algorithm is implemented using number of gates.
Beam propagation simulation¶
The ability to transform between real and Fourier domains enables us to simulate various cases of the propagation of a monochromatic field. The problem of beam propagation starts with an initial field in the transverse plane perpendicular to the direction of motion and deals with calculating the field distribution after propagating through a medium. In the following discussion, we assume one transverse direction and the propagation direction to be .
Starting with the initial field , arbitrary phase masks can be applied in the real domain by applying the phase algorithm on the register as
Phase masks also include the special case of a thin lens with the focal length where the effect of the lens can be modeled via a quadratic phase Saleh & Teich (1991) as
where λ is the wavelength of the monochromatic field.
Furthermore, the propagation of the beam for a distance in a medium having a known dispersion relation can be modeled by applying a phase transfer function to the Fourier spectrum of the field
where is derived from a dispersion relation , where is the refractive index. As long as we deal with real refractive indices and can ignore large Fourier components such that the term stays real, the transfer function is just applying a phase; hence, we can simulate the propagation using the phase algorithm acting on the Fourier representation of the field . We also note that one can use Taylor expansion to approximate the phase term in the transfer function. The most notable case is the well-known paraxial approximation where the phase term is approximated using a quadratic term Saleh & Teich (1991).
We can combine the propagation and phase mask elements in a sequence to simulate various optical experiments.
Hamiltonian simulation in quantum mechanics¶
We can also use QFT and the phase algorithm to simulate quantum mechanical systems. Assuming we start with a wavefunction stored in the quantum register
the momentum representation of this state can be calculated using the QFT as
where using de Broglie relation Broglie (1970).
This allows us to simulate any Hamiltonian consisting of a kinetic energy term as a function of the momentum operator and a potential energy term as a function of the position operator
The Hamiltonian, for example, can correspond to the harmonic oscillator where .
The unitary operator of the time evolution is thus
Using the Lie–Trotter product formula Trotter (1959), we can write the evolution operator as a sequence of individual phase operators in terms of position or momentum operators
where , and the approximation will become an equality for .
As long as is large enough to make the phase profiles and small, these phase transformations can be done using the partial phase operator. This means that we can implement the time evolution unitary by combining partial phase operators plus forward and backward QFTs. The computational complexity as a function of in this case will thus be .
Note that the phase operator applies the phase to the position representation and therefore can be implemented only using the partial phase operator. However, the phase operator applies the phase to the momentum representation, thus, we need to transform the register to the momentum representation using a QFT, apply the phase, and transform back to the real domain using an inverse QFT.
Reusing the secondary registers¶
Another interesting open question is the possibility of reusing the secondary quantum registers in the iterations of the phase algorithm. In its current form, the phase algorithm needs secondary quantum registers which are used in each iteration to apply the phase step Δ and discarded afterward. The state of each secondary register changes after the application of the partial phase operator and is slightly entangled with the primary register.
This entanglement does not allow us to reset the register by directly measuring and re-initializing it in the original state because measurement will force the entangled wavefunction of the primary and secondary registers to collapse, thus, part of the information to be lost. These registers therefore have to be kept unmeasured until the end of the phase algorithm which is unfavorable for the case of very large .
We suggest investigating the possibility of performing local operations on the secondary registers after each partial phase operation to prepare them for non-destructive measurements that do not significantly disturb the primary register. If possible, this will enable reusing the secondary registers for the next iterations, eliminating the need for a growing amount of memory proportional to the number of iterations .
Acknowledgments¶
I would like to thank my supervisors and colleagues who have supported me working on this project.
I would also like to acknowledge the support of the Max Planck School of Photonics graduate school that has offered me a scholarship during my Master’s studies enabling me to fully dedicate my focus on this research work.
The figures containing quantum circuits in the thesis were created using a LaTeX package named yquant by Benjamin Desef:
Desef, Benjamin. “Yquant: Typesetting Quantum Circuits in a Human-Readable Language.” arXiv, September 4, 2021. DOI: Desef (2020).
- Shor, P. W. (1997). Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM Journal on Computing, 26(5), 1484–1509. 10.1137/S0097539795293172
- Grover, L. K. (1996). A Fast Quantum Mechanical Algorithm for Database Search. Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, 212–219. 10.1145/237814.237866
- Montanaro, A. (2016). Quantum algorithms: an overview. Npj Quantum Information, 2(1), 15023. 10.1038/npjqi.2015.23
- Nielsen, M. A., & Chuang, I. L. (2010). Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge University Press. 10.1017/CBO9780511976667
- Saleh, B. E. A., & Teich, M. C. (1991). Electromagnetic Optics. In Fundamentals of Photonics (pp. 157–192). John Wiley & Sons, Ltd. 10.1002/0471213748.ch5